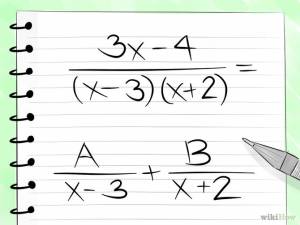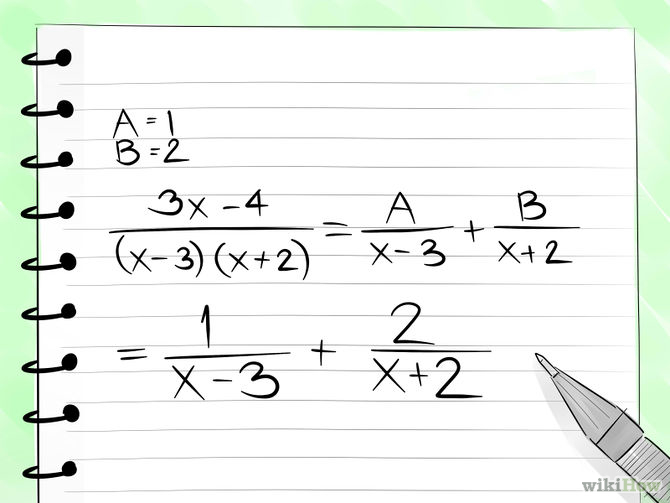Integration functions can be a little confusing especially when it involves polynomials in the denominator. In such cases use of integration fractions can be easy and can solve the problem in minutes. Students of calculus will find it handy to learn how to decompose functions into partial fractions for other parts of calculus.
- Check to make sure that the fraction you are trying to integrate is proper: A proper fraction has a smaller in the denominator than in the numerator. If the power of the numerator is larger than or equal to the power of denominator, it is improper and must be divided using long division.
- After dividing your improper fraction with long division, your new fraction can be put in the form of quotient +(remainder / divisor)
- Factor the polynomials in the denominator
- Separate the fraction that you wish to decompose in to multiple fractions: The number of fractions in decomposition should be equal to the number of factors of x. The numerators of these decomposed fractions should be represented with constants.
- Multiply both sides by the denominator of the original fraction in order to get rid of all denominators.
- Set the coefficients equal on both the sides.
These are few steps that can be used to integrate by partial fractions. People who are into calculus this function is very beneficial to them. It makes it very easy for them to calculate their problems in less time and without making it complex. Get the answers right at the very first time, once you know how to integrate by partial fraction. This principle is very useful and once we learn it then it is easy to solve problems using this technique.
Be open minded and learn how to use integrated fractions to solve your problems and you will know how easy it is once learned well. Now colleges teach this subject as well when it is necessary for the students in their said subjects. It is an interesting subject and many calculus students learn this quick and fast